Taming POV-Ray - Part 2: Manipulating Objects
by G. Moran, 17 Mar 2024
Following up on part 1, this article covers the many ways to manipulate 3D objects in POV-Ray. By learning about 3D transformations and Constructive Solid Geometry (CSG) we can make complex models out of the basic shapes that POV-Ray provides.
Table of contents
3D Transformations
In the previous article we got familiar with the 3D objects available in POV-Ray and placed a few of them into a scene, now we're going to apply some 3D transformations on them, similar to the 2D transformations we did before.
Before we do any transformations though, let me mention a little detail about the 3D coordinate system that I skipped in the previous article... Remember when I said that if the positive x axis is going right and the positive y axis is going up, then the positive z axis will go into the screen? That is not always true; sometimes the positive z axis goes out of the screen!
You see, the 3D coordinate system can follow one of two "orientation systems"; the left hand system and the right hand system. To understand how those work, make an "L" shape with your hand:

Photo by Sage Ross [CC-BY-SA]
Pretend that your thumb is the x axis and your index finger is the y axis, then align your hand to the screen so your x axis goes right and your y axis goes up... Now pretend that the z axis is coming out of your palm; if you were raising your left hand then your z axis will go into the screen, and if you were raising your right hand then your z axis will go out of the screen. That's all there is to it!
POV-Ray by default uses the left hand system, so this is what we will use. Switching to the right hand system is possible however it is outside the scope of this article.
We will do all 3D transformations directly in POV-Ray. Create a new scene with the following text:
/* 3D transformations scene */
#version 2.0
#include "colors.inc"
camera {
location <4,3,-4>
look_at <0,1,0>
}
light_source {<4, 4, -4> color White}
plane {
y, 0
pigment {checker color Black color White}
}
union {cylinder {x-x,x* 2,.1} cone {x* 2,.2,x* 3,0}
pigment {color Red}}
union {cylinder {y-y,y* 2,.1} cone {y* 2,.2,y* 3,0}
pigment {color Green}}
union {cylinder {z-z,z* 2,.1} cone {z* 2,.2,z* 3,0}
pigment {color Blue}}
union {cylinder {x-x,x*-2,.1} cone {x*-2,.2,x*-3,0}
pigment {color Magenta}}
union {cylinder {y-y,y*-2,.1} cone {y*-2,.2,y*-3,0}
pigment {color Yellow}}
union {cylinder {z-z,z*-2,.1} cone {z*-2,.2,z*-3,0}
pigment {color Cyan}}
This will give us the boilerplate scene with a camera, light source, 2D checkerboard plane (grid), and colored axes which we've seen in the previous article.
Translation
Let's add a sphere at the origin with radius 1:
sphere {
<0,0,0>, 1
pigment {color Orange}
}

The sphere is halfway inside the checkerboard plane, so we're going to translate the sphere by 1 unit (the length of the radius) in the positive y direction. In other words, we're moving the sphere "up" by 1 unit so it's completely outside the plane... We're also going to translate the sphere by 2 units along x:
sphere {
<0,0,0>, 1
pigment {color Orange}
translate <2,1,0>
}

What we did here was simply add the word translate followed by a 3D vector to our sphere {...} block, where the vector contains how many units we're translating by in the x, y, and z axes. Since we're not doing any translation in the z axis, we wrote zero in the z component of the vector.
If you're confused just raise your left hand, make an "L" shape, and align it with the screen like you did before. The way your thumb, index, and palm are pointing is where positive translation will happen along the x, y, and z axes respectively.
Rotation
A sphere is too uniform to clearly showcase rotation, so let's add a cone extending from the origin 2 units along the y axis:
cone {
<0,0,0>, 1, <0,2,0>, 0
pigment {color Yellow}
}

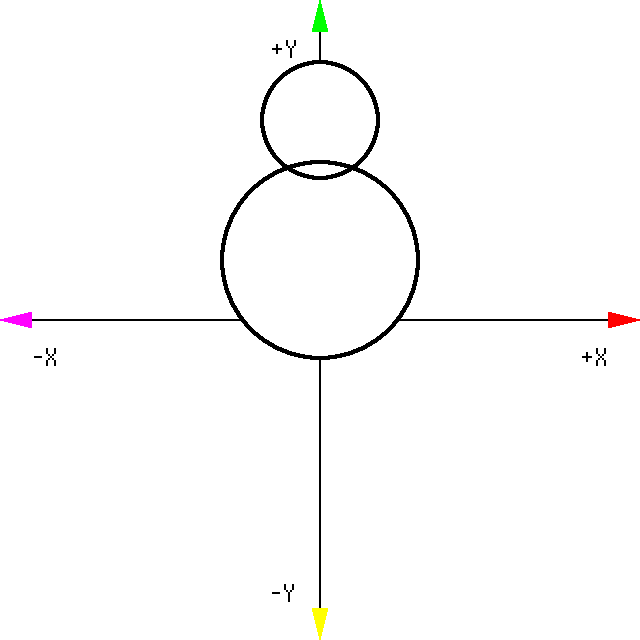
Now we're going to rotate the cone so it points along the z axis instead of the y axis. In other words, we're making the cone point "into the screen" instead of "up". To better understand what this looks like, here's a 2D view:
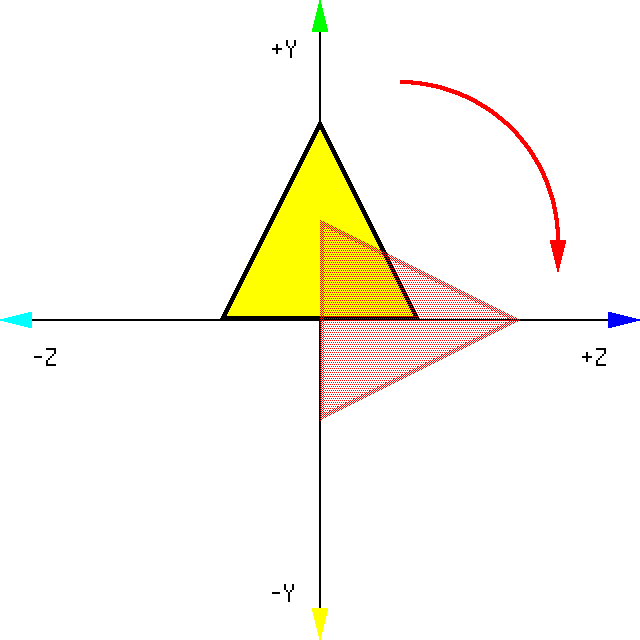
In 2D space rotation was done about the origin, but in 3D space rotation is done about the axes. Typically you would pick one axis at a time and rotate your object(s) about it, the way birds would rotate about a flag pole or lambs would rotate about a spit rod. In the case of the cone we only need to rotate about one axis; the x axis.
Now we have to determine the angle of rotation. By eye we can tell that this is an angle of 90 degrees, but is it positive or negative 90 degrees?...
Let's refer back to the left hand system introduced earlier; with your left hand make a "thumbs up" shape, then align your thumb so it's pointing along the x axis which we're rotating about. The direction your fingers curl is how positive rotation will happen about the axis, like so:

So we'll be rotating our cone by positive 90 degrees about the x axis:
cone {
<0,0,0>, 1, <0,2,0>, 0
pigment {color Yellow}
rotate x*90
}

Just like translate, the rotate keyword is followed by a 3D vector, in this case x (shorthand for <1,0,0>) multiplied by positive 90 degrees, resulting in <90,0,0>. That means rotate by 90 degrees about x, with no rotation about the other axes. I personally prefer to write x*90 because it's clearer.
Now let's say we want to rotate the cone further so it points along the negative x axis ("left"), this time we'll need to rotate about the y axis by 90 degrees. To determine the rotation sign, make a "thumbs up" shape with your left hand again and point it along the y axis; you'll find that we need to rotate 90 degrees opposite to the direction your fingers curl...
So we'll be rotating by negative 90 degrees about the y axis:
cone {
<0,0,0>, 1, <0,2,0>, 0
pigment {color Yellow}
rotate x*90
rotate y*-90
}
The rule of thumb when it comes to rotation is that you always rotate about a single axis at a time to avoid any confusion. If you write rotate <180,90,45> then POV-Ray will rotate your object by 180 degrees about x, then by 90 degrees about y, then by 45 degrees about z, which may not be what you want.
Scaling
Going back to the sphere, we're going to scale it by 0.5, basically shrinking it to half size. But if we scale it while it's away from the origin then both its size and distance from the origin will scale, when we only want to scale the size relative to the sphere center... So we're going to do the same trick outlined in the 2D article; translate the object to the origin, scale it, then translate back to the original location.
We know that the sphere's center is currently at <2,1,0> so we first need to translate it to the origin:
sphere {
<0,0,0>, 1
pigment {color Orange}
translate <2,1,0>
translate <-2,-1,0> /* move to the origin */
}

Then we're going to scale the sphere by 0.5:
sphere {
<0,0,0>, 1
pigment {color Orange}
translate <2,1,0>
translate <-2,-1,0> /* move to the origin */
scale 0.5 /* shrink to half size */
}

Then finally we're going to translate back to <2,1,0>:
sphere {
<0,0,0>, 1
pigment {color Orange}
translate <2,1,0>
translate <-2,-1,0> /* move to the origin */
scale 0.5 /* shrink to half size */
translate < 2, 1,0> /* move back */
}

Notice how the sphere, now shrunken, hovers above the plane instead of resting on top of it? That's because the center point of the sphere has not changed; it remained at <2,1,0> before and after scaling... If we wanted to keep the sphere exactly on top of the plane, we would have changed the last translation vector, specifically the y component of it, to account for the sphere's new height which was halved.
sphere {
<0,0,0>, 1
pigment {color Orange}
translate <2,1,0>
translate <-2,-1,0> /* move to the origin */
scale 0.5 /* shrink to half size */
translate <2,0.5,0> /* move above plane */
}

Alternatively, we could model the sphere to be on top of the plane from the very beginning, so we would have the freedom to enlarge or shrink the sphere without having to keep track of its y distance from the plane.
So far we have been scaling the sphere by a single factor, so the scaling happens across all 3 axes uniformly. What if we wanted to scale non-uniformly by different amounts in each axis? Then we simply replace the single factor by a vector:
sphere {
<0,0,0>, 1
pigment {color Orange}
translate <2,1,0>
translate <-2,-1,0> /* move to the origin */
scale <1,0.5,1> /* shrink to half height */
translate <2,0.5,0> /* move above plane */
}
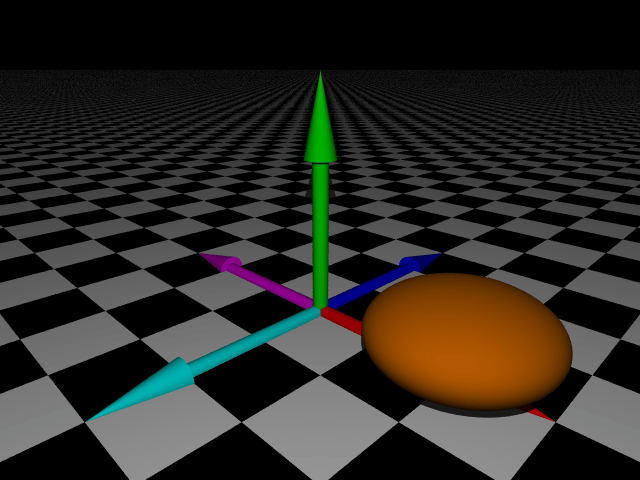
As you can see, the sphere has been squashed. That's because we only scaled along the y axis by a factor of 0.5, with no scaling along the other axes. Recall from the 2D article that a scaling factor of 1 means no scaling, which is why the x and z components of the scaling vector are 1.
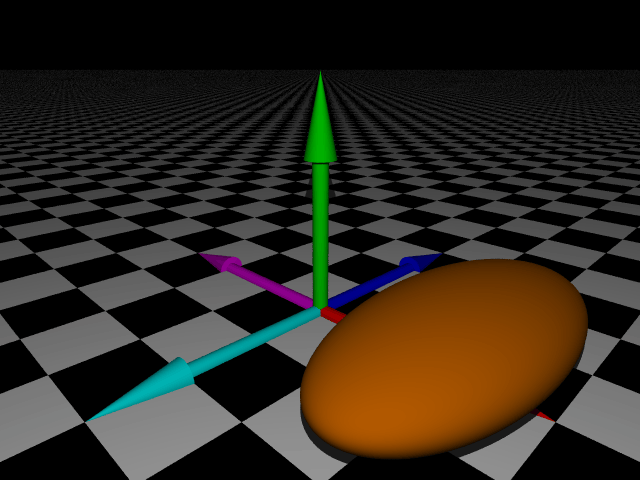
We can use non-uniform scaling to distort shapes in many ways.
sphere {
<0,0,0>, 1
pigment {color Orange}
translate <2,1,0>
translate <-2,-1,0> /* move to the origin */
scale <1,0.5,2> /* x0.5 height, x2 depth */
translate <2,0.5,0> /* move above plane */
}
Constructive Solid Geometry (CSG)
POV-Ray's basic shapes are nice and all, but we could create more elaborate shapes by manipulating multiple objects together. For example we could group two objects and transform them as one, or subtract one object from another, or intersect multiple objects... These operations are called Constructive Solid Geometry (CSG).
Here's a quick 2D visualizer of the CSG operations we can do:
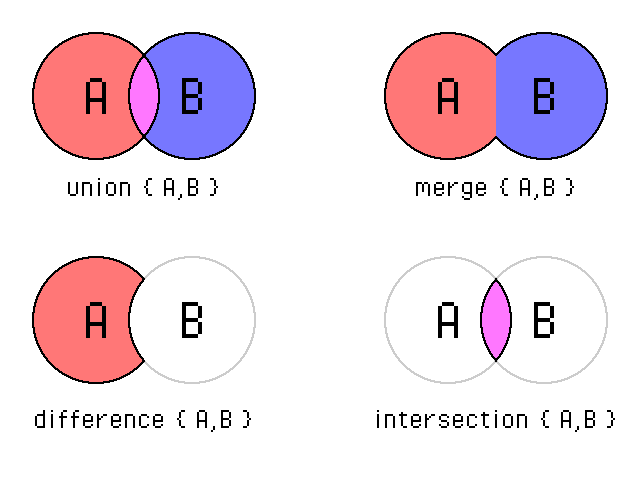
We will go over each of these operations in detail and apply them to different objects in POV-Ray, with each operation creating a new shape. We're also going to remove the colored axes to better see our objects.
Union
Union is the simplest CSG operation there is; it groups multiple objects together. Once grouped, the objects in the union are treated as one object...
Let's say we want to build a basic snowman with a head and a body, both colored white, so that he looks something like this:
All we have to do is enclose two spheres in a union {...} block, then give the union a color:
union {
sphere {<0,0.6,0>, 1} /* snowman body */
sphere {<0,2,0>, 0.6} /* snowman head */
pigment {color White}
}

Notice how specifying a color in the union automatically applies it to all the objects inside? This also goes for 3D transformations and other CSG operations.
How about giving the snowman a hat?
Let's model one out of cylinders near the origin, then lift it up above the snowman's head and give it a nice golden color.
union {
sphere {<0,0.6,0>, 1} /* snowman body */
sphere {<0,2,0>, 0.6} /* snowman head */
pigment {color White}
}
union {
cylinder {<0,0,0>, <0,0.1,0>, 0.9} /* hat base */
cylinder {<0,0,0>, <0,1.0,0>, 0.5} /* hat top */
translate y*2.5
pigment {color Gold}
}

We now have two unions for the snowman and his hat, but what if we want to manipulate the snowman with his hat? Simple; we enclose the two unions in another union {...} block:
union {
union { /* snowman */
sphere {<0,0.6,0>, 1}
sphere {<0,2,0>, 0.6}
pigment {color White}
}
union { /* hat */
cylinder {<0,0,0>, <0,0.1,0>, 0.9}
cylinder {<0,0,0>, <0,1.0,0>, 0.5}
translate y*2.5
pigment {color Gold}
}
translate z*6 /* move them both */
}

CSG operations can be nested like this to create all sorts of combinations, we will see more examples of this later on.
Merge
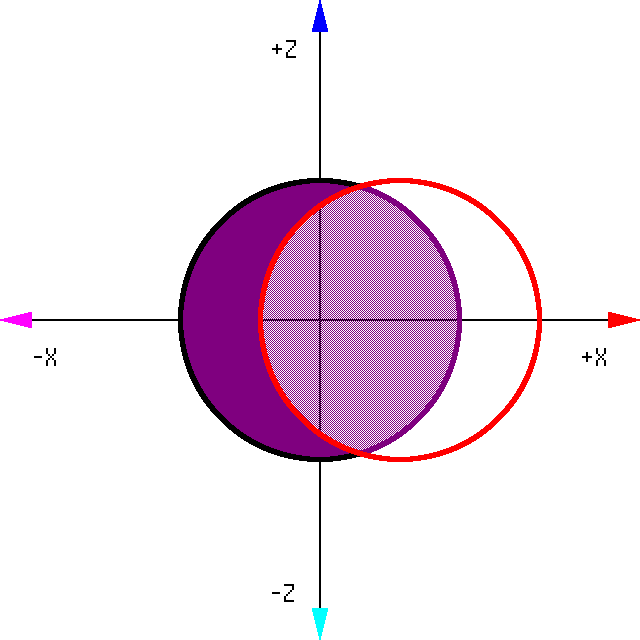
Merge is almost exactly like Union but with one difference; if the objects overlap, the parts that are overlapping are "merged" together... The best way to explain it is with an example:
We're going to model this martini glass with overlapping shapes, where the overlaps are indicated in dark blue, once as a union and once as a merge. We're also going to make the glass transparent, so we can see the overlaps more clearly.
Here's the glass as a union:
union {
cone {<0,0,0>, 0.6, <0,0.3,0>, 0.2 open} /* base */
cylinder {<0,0,0>, <0,3,0>, 0.2 open} /* neck */
cone {<0,2,0>, 0.2, <0,3,0>, 1 open} /* head */
pigment {color Cyan filter 0.5}
}

Here we added the keyword filter after the color to make it transparent, followed by a number indicating the transparency level. 0 is fully opaque and 1 is fully transparent, so this glass is half transparent.
Notice how the glass' neck, which overlaps the head and base, is fully visible?..
Now here's the same glass as a merge:
merge {
cone {<0,0,0>, 0.6, <0,0.3,0>, 0.2 open} /* base */
cylinder {<0,0,0>, <0,3,0>, 0.2 open} /* neck */
cone {<0,2,0>, 0.2, <0,3,0>, 1 open} /* head */
pigment {color Cyan filter 0.5}
}

The overlaps are no longer visible, and the glass looks much more natural. All we did was replace union with merge, the geometry of the glass is exactly the same.
Difference
Difference is essentially subtracting one or more objects from an initial object.
To demonstrate this we're going to model a crescent:

This shape is nothing more than a circle, with another circler subtracted out of it, like this:
Let's start by creating the first circle as a cylinder:
/* first circle */
cylinder {
<0,0,0>, <0,0.5,0>, 2
pigment {color Magenta}
}

Then we will enclose the cylinder in a difference block and add another cylinder after it to create a hole. Pay attention to the ordering here; the shape we're subtracting from is added to the difference block first, and any following shapes are subtracted from it to create holes.
difference {
/* first circle */
cylinder { <0,0,0>, <0,0.5,0>, 2 }
/* hole */
cylinder { <1,0,0>, <1,0.5,0>, 2 }
pigment {color Magenta}
}

Huh, that's strange... Where is the hole?
The hole is right there, in fact you can see that the cylinder is hollow from the side, however the hole does not reach the top of the cylinder. That's because both the cylinder and the hole have the exact same height, so the area at the top is simultaneously "filled" and "empty", same goes for the area at the bottom. Such areas are in an undefined state and may be rendered by the raytracer as filled, empty, or a mixture of both...
To eliminate those areas and get a proper crescent, we simply have to extend the shape of the hole above and below the cylinder:
difference {
/* first circle */
cylinder { <0, 0,0>, <0,0.5,0>, 2 }
/* extended hole */
cylinder { <1,-1,0>, <1, 1,0>, 2 }
pigment {color Magenta}
}

We can add more shapes to the difference block and each one will create another hole in the first shape. Note that additional shapes must overlap the first shape for any holes to be created.
Intersection
Intersection is essentially the area common between two or more overlapping objects.
To demonstrate this we're going to model this eye-like shape:
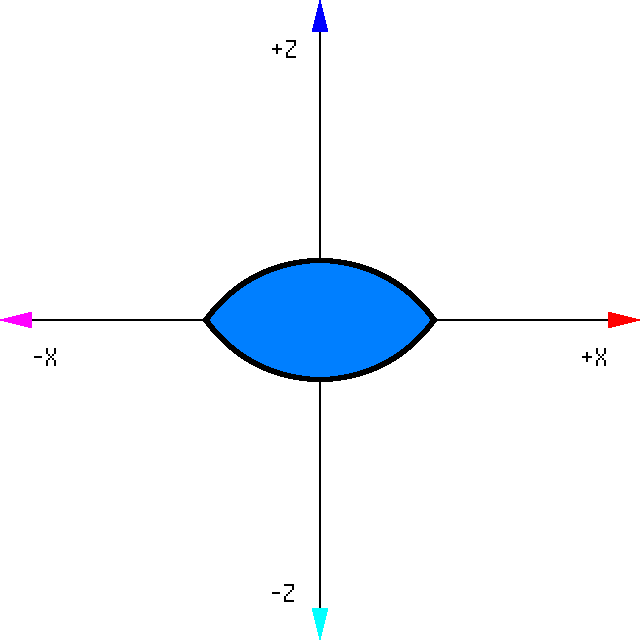
This shape is nothing more than the overlap between 2 circles:
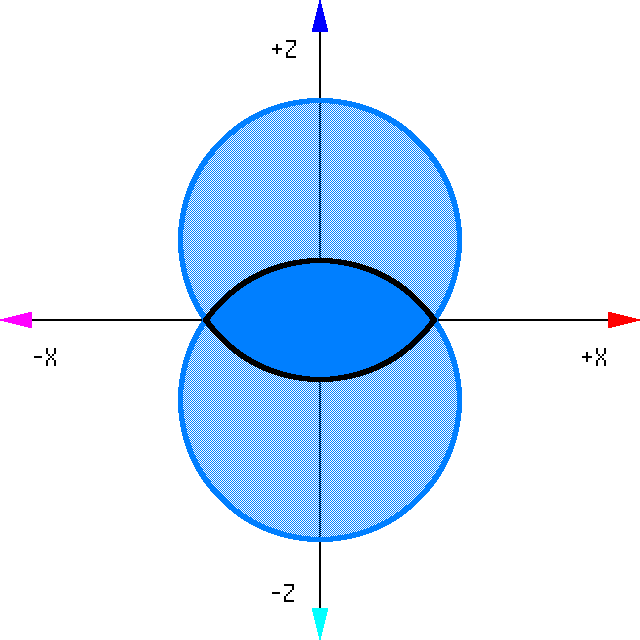
To model this shape we will create 2 overlapping cylinders and enclose them in an intersection block. The ordering doesn't matter here, any order will achieve the same effect.
intersection {
/* first circle */
cylinder { <0,0, 1>, <0,0.5, 1>, 2 }
/* second circle */
cylinder { <0,0,-1>, <0,0.5,-1>, 2 }
pigment {color SlateBlue}
}

We can add more (overlapping) shapes to the intersection block and only the area common between all shapes will be rendered.
CSG-compatible objects
CSG operations (other than union) only work on solid objects, meaning objects that are filled and have a clear "inside" and "outside". Spheres, boxes, cylinders, cones, planes...etc are solid. Triangles and triangulated surfaces (bicubic patches, height fields) are not solid, they have no real thickness so they don't have an "inside" nor an "outside".
In some cases it's possible to perform CSG operations between a triangulated surface and a solid object, but CSG operations purely between triangulated surfaces is invalid and will result in an error.
Declarations
Sometimes you'll want to render an object more than once, for that you have two options; either model the object over and over (tedious, error-prone, wastes space), or model the object only once and simply reference it multiple times. The latter option is made possible by the #declare keyword.
To declare any object, simply add #declare MyObject = before the object's block. This declaration stores the object in memory and gives it the name MyObject, without rendering it. To render the declared object, simply add object {MyObject ...} into your scene.
To better illustrate this concept, we will create a scene containing the 3 pyramids of Giza. We will start by modeling a single pyramid like so:
/* extra light */
light_source {<0, 2, -4> color Gray}
/* pyramid */
difference {
box {<-1,0,-1>, <1,1,1>}
plane {-x-y, 0 translate x}
plane { x-y, 0 translate -x}
plane {-z-y, 0 translate z}
plane { z-y, 0 translate -z}
pigment {color Gold}
}

The pyramid is nothing more than a box with 4 tilted walls subtracted from it, I added an additional light source to the scene so you can better see the shape.
Now we're going to declare this shape and give it a name; Pyramid. You can choose any name you like as long as it's not a POV-Ray keyword. Since the shape is modeled by a difference block, we will add #declare Pyramid = before it:
/* pyramid */
#declare Pyramid = difference {
box {<-1,0,-1>, <1,1,1>}
plane {-x-y, 0 translate x}
plane { x-y, 0 translate -x}
plane {-z-y, 0 translate z}
plane { z-y, 0 translate -z}
pigment {color Gold}
}
Remember, if we render our scene now the pyramid will not be rendered! All we did was name a shape and store it in memory, it is not added to the scene... So to add it, we will reference it by name in an object {...} block:
object {Pyramid}

The pyramid is back in our scene, exactly as it was modeled. But that's not our goal, our goal is to have 3 pyramids in different locations. So let's reference the pyramid 2 more times, and translate each reference separately.
object {Pyramid translate 2*x}
object {Pyramid}
object {Pyramid translate -2*x}

Very good, however the pyramids are all the exact same size. Let's scale each pyramid independently before translating it. Note here that the scaling is done before the translation, as we always scale objects at the origin.
object {Pyramid scale 1.5 translate 2.5*x}
object {Pyramid}
object {Pyramid scale 0.5 translate -1.5*x}

That's more like it.
Declarations are a powerful tool that greatly facilitates scene writing, and they can be used with all sorts of POV-Ray data, not just objects. Here are some examples:
#declare Height = 12
#declare BrightBlue = color rgb <0.3, 0.5, 1.0>
#declare ChessTiles = pigment {
checker color Black color White
}
We will see more examples of declarations in the upcoming articles.
Include Files
Another powerful feature of POV-Ray is the ability to include files in other files. Since the last article we have been including a file named colors.inc at the top of our scenes, this file declares a large number of colors that we can reference directly by name. Having all colors declared in a separate file allows us to include it into multiple scenes, without having to manually declare the colors each time... Also, not only do we get to reuse code by keeping it in a separate file, we also get to keep our scene file focused and uncluttered. It's much easier to reason about a group of clearly named files, than a single giant file with a wall of code inside.
A good convenient way to structure your scenes is as follows:
- Create one file for your scene, named
scene.povfor example. This is the main file that you will feed into POV-Ray to render. - Create separate files for declaring each (non-trivial) object you model;
obj1.inc,obj2.inc,obj3.inc...etc. - Include each object in your scene by adding
#include obj1.inc,#include obj2.inc...etc at the top of thescene.povfile. - Avoid including
*.incfiles in other*.incfiles, as that can easily lead to a network of includes that is hard to debug, or "circular includes" (file A includes file B, and file B includes file A) that crash POV-Ray.
Wrapping Up
Now you should know how to manipulate shapes using 3D transformations, combine shapes using CSG operations, declare objects, and include files in other files. In the next article we'll learn how to give our shapes colors and textures, until then feel free to play around with POV-Ray and practice what you learned.